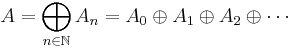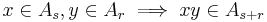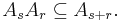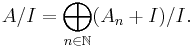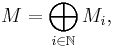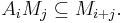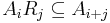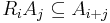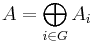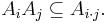Graded algebra

In mathematics, in particular abstract algebra, a graded algebra is an algebra over a field (or commutative ring) with an extra piece of structure, known as a gradation (or grading).

The grading is a direct sum decomposition of the algebra with factors indexed in a special way by a monoid. Given a pair of elements from two factors of the grading, the indexing allows one to know which factor of the grading will contain the product of the chosen elements.

Contents

Graded rings

A graded ring A is a ring that has a direct sum decomposition into (abelian) additive groups

A = \bigoplus_{n\in \mathbb N}A_n = A_0 \oplus A_1 \oplus A_2 \oplus \cdots

such that the ring multiplication satisfies

x \in A_s, y \in A_r \implies xy \in A_{s%2Br}

and so

A_s A_r \subseteq A_{s %2B r}.

Elements of 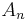A_n are known as homogeneous elements of degree n. An ideal or other subset 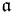\mathfrak{a} ⊂ A is homogeneous if for every element a ∈ 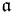\mathfrak{a}, the homogeneous parts of a are also contained in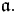 \mathfrak{a}.

If I is a homogeneous ideal in A, then 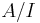A/I is also a graded ring, and has decomposition

A/I = \bigoplus_{n\in \mathbb N}(A_n %2B I)/I.

Any (non-graded) ring A can be given a gradation by letting A0 = A, and Ai = 0 for i > 0. This is called the trivial gradation on A.

Graded modules

The corresponding idea in module theory is that of a graded module, namely a module M over a graded ring A such that also

M = \bigoplus_{i\in \mathbb N}M_i ,

and

A_iM_j \subseteq M_{i%2Bj}.

This idea is much used in commutative algebra, and elsewhere, to define under mild hypotheses a Hilbert function, namely the length of Mn as a function of n. Again under mild hypotheses of finiteness, this function is a polynomial, the Hilbert polynomial, for all large enough values of n.

Graded algebras

An algebra A over a ring R is a graded algebra if it is graded as a ring. In the case where the ring R is also a graded ring, then one requires that

A_iR_j \subseteq A_{i%2Bj}

and

R_iA_j \subseteq A_{i%2Bj}

Note that the definition of the graded ring over a ring with no grading is the special case of the latter definition where "R" is given the trivial grading (every element of "R" is of grade 0).

Examples of graded algebras are common in mathematics:

Graded algebras are much used in commutative algebra and algebraic geometry, homological algebra and algebraic topology. One example is the close relationship between homogeneous polynomials and projective varieties.

G-graded rings and algebras

We can generalize the definition of a graded ring using any monoid G as an index set. A G-graded ring A is a ring with a direct sum decomposition

A = \bigoplus_{i\in G}A_i

such that

A_i A_j \subseteq A_{i \cdot j}.

The notion of "graded ring" now becomes the same thing as a N-graded ring, where N is the monoid of non-negative integers under addition. The definitions for graded modules and algebras can also be extended this way replacing the indexing set N with any monoid G.

Remarks:

Examples:

In category theory, a G-graded algebra A is an object in the category of G-graded vector spaces, together with a morphism 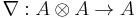\nabla:A\otimes A\rightarrow A of the degree of the identity of G.

Anticommutativity

Some graded rings (or algebras) are endowed with an anticommutative structure. This notion requires the use of a semiring to supply the gradation rather than a monoid. Specifically, a signed semiring consists of a pair (Γ, ε) where Γ is a semiring and ε : Γ → Z/2Z is a homomorphism of additive monoids. An anticommutative Γ-graded ring is a ring A graded with respect to the additive structure on Γ such that:

xy=(-1)ε (deg x) ε (deg y)yx, for all homogeneous elements x and y.

Examples

See also

References